142,857, 142,857, 142,857

142 857: 142857, šest opakující číslice 1/7, 0 142857, je nejznámější cyklický číslo v základně 10. Pokud se násobí 2, 3, 4, 5, nebo 6, odpověď bude cyklický permutace sám, a bude odpovídat opakujících číslic 2/7, 3/7, 4/7, 5/7 nebo 6/7, resp.
142 857: 142857, šest opakující číslice 1/7, 0 142857, je nejznámější cyklický číslo v základně 10. Pokud se násobí 2, 3, 4, 5, nebo 6, odpověď bude cyklický permutace sám, a bude odpovídat opakujících číslic 2/7, 3/7, 4/7, 5/7 nebo 6/7, resp.
142 857: 142857, šest opakující číslice 1/7, 0 142857, je nejznámější cyklický číslo v základně 10. Pokud se násobí 2, 3, 4, 5, nebo 6, odpověď bude cyklický permutace sám, a bude odpovídat opakujících číslic 2/7, 3/7, 4/7, 5/7 nebo 6/7, resp.
142 857: 142857, šest opakující číslice 1/7, 0 142857, je nejznámější cyklický číslo v základně 10. Pokud se násobí 2, 3, 4, 5, nebo 6, odpověď bude cyklický permutace sám, a bude odpovídat opakujících číslic 2/7, 3/7, 4/7, 5/7 nebo 6/7, resp.
Ráže .177: Kalibr 0,177 nebo 4,5 mm je nejmenší průměr pelet a broků BB široce používaných ve vzduchových zbraních a je jediným kalibrem obecně přijímaným pro formální cílovou soutěž. Někdy se také používá k lovu malé zvěře, stejně jako v terénu, kde soutěží s puškami ráže 5 mm a 0,22 (5,5 mm).
.17 Remington Fireball: 0,17 Remington Fireball byl vytvořen v roce 2007 společností Remington Arms Company jako reakce na populární divoké kolo, 0,17 Mach IV. Tovární zátěže pohánějí kulku o hmotnosti 20 g (1,3 g) kolem 419 ft / s (1219 m / s). Rychlost se blíží 0,17 Remingtonu, ale s podstatně menším množstvím prášku, a tedy méně tepla a znečištění. Oba jsou důležitým problémem pro velkoobjemové střelce, jako jsou lovci varmintů.
.17 Remington: 0,17 Remington byl představen v roce 1971 společností Remington Arms Company pro své pušky modelu 700.
.17 Remington Fireball: 0,17 Remington Fireball byl vytvořen v roce 2007 společností Remington Arms Company jako reakce na populární divoké kolo, 0,17 Mach IV. Tovární zátěže pohánějí kulku o hmotnosti 20 g (1,3 g) kolem 419 ft / s (1219 m / s). Rychlost se blíží 0,17 Remingtonu, ale s podstatně menším množstvím prášku, a tedy méně tepla a znečištění. Oba jsou důležitým problémem pro velkoobjemové střelce, jako jsou lovci varmintů.
.17 Remington: 0,17 Remington byl představen v roce 1971 společností Remington Arms Company pro své pušky modelu 700.
180 nm proces: Proces 180 nm se týká úrovně technologie polovodičových procesů MOSFET (CMOS), která byla komercializována v časovém rámci 1998–2000 předními polovodičovými společnostmi, počínaje TSMC a Fujitsu, poté následovaly společnosti Sony, Toshiba, Intel, AMD, Texas Instruments a IBM.
Řádové řády (oblast): Tato stránka je progresivní a označený seznam řádových oblastí oblasti SI, s některými příklady připojenými k některým objektům seznamu.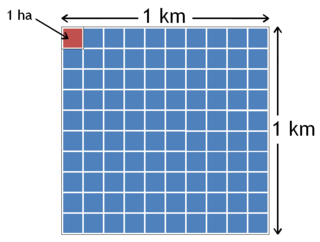
.20 Taktické: 0,20 Tactical je divoká nábojová puška se středovým zápalem, založená na pouzdru 0,223 Remington, s hrdlem dolů, aby vystřelila kulku ráže 5,2 milimetru (0,204 palce). 0,20 Tactical navrhl Todd Kindler a předchází tovární kolo .204 Ruger. Pouzdro má přibližně o 0,2 gramu (3 g) menší kapacitu prášku než populární .204 Ruger. Ruční nakladače mohou získat rychlosti s projektily 2,1 a 2,6 gramů, které téměř odpovídají rageru .204 Ruger. Kromě toho je 0,20 Tactical schopen dosáhnout těchto rychlostí s menším množstvím prášku než 0,204 Ruger efektivnějším používáním vysoce energetických pohonných látek, jako jsou Alliant Reloader 7 a Winchester 748. Na základě 0,223 Remington je široký výběr mosazi k dispozici a lze je také vytvořit z pouzder .223 pomocí formovací matrice.
.20 Taktické: 0,20 Tactical je divoká nábojová puška se středovým zápalem, založená na pouzdru 0,223 Remington, s hrdlem dolů, aby vystřelila kulku ráže 5,2 milimetru (0,204 palce). 0,20 Tactical navrhl Todd Kindler a předchází tovární kolo .204 Ruger. Pouzdro má přibližně o 0,2 gramu (3 g) menší kapacitu prášku než populární .204 Ruger. Ruční nakladače mohou získat rychlosti s projektily 2,1 a 2,6 gramů, které téměř odpovídají rageru .204 Ruger. Kromě toho je 0,20 Tactical schopen dosáhnout těchto rychlostí s menším množstvím prášku než 0,204 Ruger efektivnějším používáním vysoce energetických pohonných látek, jako jsou Alliant Reloader 7 a Winchester 748. Na základě 0,223 Remington je široký výběr mosazi k dispozici a lze je také vytvořit z pouzder .223 pomocí formovací matrice.
0,222 Remington: 0,222 Remington , známý také jako trojitá dvojka , trojitá dvojka a trojka , je nábojnice s puškou na střed. Představený v roce 1950 se jednalo o první komerční kazetu bez ráfku 0,22 (5,56 mm) vyrobenou ve Spojených státech. Jako takový to byl zcela nový design, bez rodičovské skříně. 0,222 Remington byl oblíbenou cílovou kazetou od jejího zavedení až do poloviny 70. let a stále se těší reputaci přesnosti. Zůstává oblíbenou kazetou nebo „varmintovou" kazetou na krátký a střední rozsah s preferovanou hmotností střely 40–55 zrn a úsťovými rychlostmi od 3 000 do 3 500 ft / s (915–1 067 m / s).
0,222 Remington: 0,222 Remington , známý také jako trojitá dvojka , trojitá dvojka a trojka , je nábojnice s puškou na střed. Představený v roce 1950 se jednalo o první komerční kazetu bez ráfku 0,22 (5,56 mm) vyrobenou ve Spojených státech. Jako takový to byl zcela nový design, bez rodičovské skříně. 0,222 Remington byl oblíbenou cílovou kazetou od jejího zavedení až do poloviny 70. let a stále se těší reputaci přesnosti. Zůstává oblíbenou kazetou nebo „varmintovou" kazetou na krátký a střední rozsah s preferovanou hmotností střely 40–55 zrn a úsťovými rychlostmi od 3 000 do 3 500 ft / s (915–1 067 m / s).
.22 Urychlovač: Akcelerátor .22 je speciální náplň kazet .30-30, .308 a .30-06 vyráběná společností Remington.
0,22 BB: 0,22 BB Cap, také známý jako 6mm Flobert , je paleta malorážky ráže .22. Vynalezl Louis-Nicolas Flobert v roce 1845 a byla to první kovová nábojnice s okrajovým ohněm. 0,22 BB Cap a 0,22 CB Cap jsou zaměnitelné a jsou relativně tiché kazety s nízkou rychlostí, určené pro střelbu na vnitřní terč.
0,22 BR Remington: Kazeta 0,22 Bench Rest Remington , běžně označovaná jako 0,22 BR Remington , je kazeta divoké kočky běžně používaná při lovu varmintů a střelbě na lavičce. Je založen na kazetě Barnes 0,308 × 1,5 palce, zúžené na ráži 0,22, prodloužené o 0,020 palce a se sklonem ramene zvýšeným na 30 °. Poprvé byl vyvinut přibližně v roce 1963 Jimem Steklem a v roce 1978 Remington standardizoval rozměry. Je proslulý svými vysokými rychlostmi a vynikající přesností.
0,22 CB: Uzávěr 0,22 CB je výkonnější verzí kovového náboje s okrajovým ohněm 0,22 BB, který vynalezl Louis-Nicolas Flobert v roce 1845. Uzávěr 0,22 BB a uzávěr 0,22 CB jsou zaměnitelné a jsou relativně tiché, s nízkou rychlostí kazety, určené pro střelbu na vnitřní terč.
0,22 CB: Uzávěr 0,22 CB je výkonnější verzí kovového náboje s okrajovým ohněm 0,22 BB, který vynalezl Louis-Nicolas Flobert v roce 1845. Uzávěr 0,22 BB a uzávěr 0,22 CB jsou zaměnitelné a jsou relativně tiché, s nízkou rychlostí kazety, určené pro střelbu na vnitřní terč.
.22 Eargesplitten Loudenboomer: 0,22 Eargesplitten Loudenboomer je kazeta s puškou divoká.
.22 Extra dlouhé: 0,22 Extra Long je 0,22 palce (5,6 mm) americká malorážka a nábojnice.
.22 Hornet: Hornet 0,22 nebo 5,6 × 35 mmR je varminting, lov na malé zvěře, přežití a soutěž s náboji na střed, který byl komerčně představen v roce 1930. Je podstatně výkonnější než malorážka 0,22 WMR a 0,17 HMR, dosahující vyšší rychlosti s střela dvakrát větší než střela 0,17 HMR. Hornet se od nich také velmi výrazně liší v tom, že díky náboji se středovým ohněm se dá dobíjet a znovu nabíjet, a tedy mnohem univerzálnější. Jednalo se o nejmenší komerčně dostupnou kazetu s ráží 0,22 ráže až do zavedení FN 5,7 × 28 mm.
0,22 dlouhé: 0,22 Long je paleta malorážky ráže 0,6 mm (5,6 mm). 0,22 Long je druhou nejstarší z dochovaných malorážkových nábojů, která sahá až do roku 1871, kdy byla nabitá kulkou s 29 zrny a 5 zrny černého prachu, což je o 25% více než na základě .22 Short. Byl navržen pro použití v revolverech, ale brzy byl také vybaven puškami, ve kterých získal silnou reputaci jako malá herní kazeta a prodával se velmi dobře.
0,22 Dlouhá puška: 0,22 Long Rifle nebo jednoduše 0,22 LR je dlouho zavedená odrůda malorážky malorážky ráže .22 pocházející ze Spojených států. Používá se v široké škále pušek, pistolí, revolverů, brokovnic s hladkým vývrtem a samopalů.
0,22 PPC: 0,22 PPC je nábojnice s puškou na střed, vyvinutá v roce 1974 Dr. Louisem Palmisanem a Ferrisem Pindellem, především jako kazeta pro benchrest. Kazeta vychází z pouzdra 5,6 × 39 mm, což je verze se sovětskou vojenskou kazetou 7,62 x 39 mm s hrdlem. Několik společností vyrobilo v tomto kalibru zakázkové zbraně, ale žádné velké společnosti to neudělaly až do roku 1993, kdy Ruger oznámil své varmintové pušky číslo 1 V a M77 v tomto kalibru.
0,22 Remington Jet: 0,22 Remington Jet je 0,22 palce (5,6 mm) americký revolver a nábojnice s puškou.
.22 Savage Hi-Power: Kazeta 0,22 Savage Hi-Power byla vytvořena Charlesem Newtonem a představena společností Savage Arms v roce 1912. Byla navržena pro použití v akční pušce Savage Model 99 bez kladiva. Je založen na kazetě Winchester 0,25-35 se zúženým hrdlem pro přijetí kulky o průměru 0,227 palce / 0,228 palce. Jeho původní náplní byla kulička s měkkým hrotem se 70 zrny o rychlosti asi 2790 stop za sekundu.
.22 Krátký: 0,22 Short je paleta malorážky ráže 0,6 mm (5,6 mm). 0,22 rimfire byl vyvinut v roce 1857 pro první revolver Smith & Wesson a byl první americkou kovovou kazetou. Původní náplň byla 29 nebo 30 g kulka a 4 g černého prachu. Původní náboj 0,22 rimfire byl přejmenován na 0,22 Short zavedením 0,22 Long v roce 1871.
.22 Spitfire: 0,22 Spitfire je americká nábojnice.
.22 TCM: 0,22 TCM nebo 22TCM je patentovaná kazeta s láhvovým hrdlem vytvořená z kazety NATO 5,56 vyvinuté zakázkovým puškařem Fredem Craigem a Rock Island Armory (RIA) pro poloautomatické pistole a pušky Rock Island M22 TCM se šroubem. Před uvedením kazety na trh se jí říkalo 22 Micro-Mag . Koncepčně podobně jako jiné pistolové náboje s hrdlem na láhve, jako je například větší kalibr 0,357 SIG, obchoduje 0,22 TCM s hmotou střely pro zvýšení rychlosti a snížení zpětného rázu.
0,22 Winchester Magnum Rimfire: 0,22 Winchester Magnum Rimfire , nazývaný také 0,22 WMR , 0,22 Magnum , 0,22 WMRF , 0,22 MRF nebo 0,22 Mag , je kazeta s okrajovým ohněm . Původně nabitý střelou o hmotnosti 40 zrn (2,6 g) dodávající rychlosti v rozsahu 2 000 stop za sekundu (610 m / s) od hlavně pušky, je nyní 0,22 WMR nabitý hmotností střely od 50 zrn (3,2 g) při 1530 stopách za sekundu (470 m / s) na 30 zrn (1,9 g) při 2200 stopách za sekundu (670 m / s).
0,22 Winchester Automatic: 0,22 Winchester Automatic je 0,22 palce (5,6 mm) americký malorážka nábojnice.
0,22 Winchester Magnum Rimfire: 0,22 Winchester Magnum Rimfire , nazývaný také 0,22 WMR , 0,22 Magnum , 0,22 WMRF , 0,22 MRF nebo 0,22 Mag , je kazeta s okrajovým ohněm . Původně nabitý střelou o hmotnosti 40 zrn (2,6 g) dodávající rychlosti v rozsahu 2 000 stop za sekundu (610 m / s) od hlavně pušky, je nyní 0,22 WMR nabitý hmotností střely od 50 zrn (3,2 g) při 1530 stopách za sekundu (470 m / s) na 30 zrn (1,9 g) při 2200 stopách za sekundu (670 m / s).
.22 Winchester Rimfire: 0,22 Winchester Rimfire je americký náboj s malorážkou.
Ráže .22: Kalibr 22 nebo 5,6 mm označuje běžný průměr otvoru střelných zbraní 5,6 mm.
Čtvrťák: Čtvrtina je jedna čtvrtina, ¼, 25% nebo 0,25.
250 nm proces: Proces 250 nm označuje úroveň technologie polovodičových procesů MOSFET (CMOS), kterou komercializovali výrobci polovodičů v časovém rámci 1996–1998.
.20 Taktické: 0,20 Tactical je divoká nábojová puška se středovým zápalem, založená na pouzdru 0,223 Remington, s hrdlem dolů, aby vystřelila kulku ráže 5,2 milimetru (0,204 palce). 0,20 Tactical navrhl Todd Kindler a předchází tovární kolo .204 Ruger. Pouzdro má přibližně o 0,2 gramu (3 g) menší kapacitu prášku než populární .204 Ruger. Ruční nakladače mohou získat rychlosti s projektily 2,1 a 2,6 gramů, které téměř odpovídají rageru .204 Ruger. Kromě toho je 0,20 Tactical schopen dosáhnout těchto rychlostí s menším množstvím prášku než 0,204 Ruger efektivnějším používáním vysoce energetických pohonných látek, jako jsou Alliant Reloader 7 a Winchester 748. Na základě 0,223 Remington je široký výběr mosazi k dispozici a lze je také vytvořit z pouzder .223 pomocí formovací matrice.
.20 Taktické: 0,20 Tactical je divoká nábojová puška se středovým zápalem, založená na pouzdru 0,223 Remington, s hrdlem dolů, aby vystřelila kulku ráže 5,2 milimetru (0,204 palce). 0,20 Tactical navrhl Todd Kindler a předchází tovární kolo .204 Ruger. Pouzdro má přibližně o 0,2 gramu (3 g) menší kapacitu prášku než populární .204 Ruger. Ruční nakladače mohou získat rychlosti s projektily 2,1 a 2,6 gramů, které téměř odpovídají rageru .204 Ruger. Kromě toho je 0,20 Tactical schopen dosáhnout těchto rychlostí s menším množstvím prášku než 0,204 Ruger efektivnějším používáním vysoce energetických pohonných látek, jako jsou Alliant Reloader 7 a Winchester 748. Na základě 0,223 Remington je široký výběr mosazi k dispozici a lze je také vytvořit z pouzder .223 pomocí formovací matrice.
0,303 Britové: 0,303 British nebo 7,7 × 56 mmR , je 0,303 palce (7,7 mm) náboj s ráfkem , který byl poprvé vyvinut v Británii jako černý práškový náboj uvedený do provozu v prosinci 1888 pro pušku Lee-Metford. V roce 1891 byla kazeta upravena pro použití bezdýmného prachu. Jednalo se o standardní vojenský náboj Britů a Commonwealthu od roku 1889 do padesátých let, kdy byl nahrazen NATO o rozměrech 7,62 × 51 mm.
Třetí: Třetí nebo třetí může odkazovat na:
0,338 Lapua Magnum: 0,338 Lapua Magnum je bezokrajová nábojová puška s úzkým hrdlem a středovým ohněm. Byl vyvinut v 80. letech jako vysoce výkonná kazeta s dlouhým doletem pro vojenské odstřelovače. To bylo používáno ve válce v Afghánistánu a válce v Iráku. V důsledku toho se stal široce dostupným. Plněná kazeta má průměr (okraj) 14,93 mm (0,588 palce) a délku 93,5 mm (3,68 palce). Dokáže proniknout lépe než standardní vojenské neprůstřelné vesty na vzdálenost až 1 000 metrů (1090 yardů) a má maximální efektivní dosah asi 1750 metrů (1910 yardů) s municí vyhovující CIP v podmínkách hladiny moře. Úsťová rychlost závisí na délce hlavně, hloubce sezení a náplni prášku a pohybuje se od 880 do 915 m / s u komerčních zátěží s kulkami 16,2 gramů (250 gr), což odpovídá asi 6 525 J (4 813 ft⋅lbf) energie tlamy.
0,357: .357 může odkazovat se na: 0,357 Magnum, nábojnice (revolver) 0,357 SIG, nábojnice (pistole) 0,357 Maximum, náboj divoká kočka (revolver)
0,357 Magnum: 0,357 Smith & Wesson Magnum , 0,357 S&W Magnum , 0,357 Magnum nebo 9 × 33 mmR, jak je známo v neoficiálním metrickém označení, je bezdýmný prachový náboj s průměrem střely 0,357 palce (9,07 mm). Vytvořili jej Elmer Keith, Phillip B. Sharpe a Douglas B. Wesson z výrobců střelných zbraní Smith & Wesson a Winchester.
0,357 Magnum: 0,357 Smith & Wesson Magnum , 0,357 S&W Magnum , 0,357 Magnum nebo 9 × 33 mmR, jak je známo v neoficiálním metrickém označení, je bezdýmný prachový náboj s průměrem střely 0,357 palce (9,07 mm). Vytvořili jej Elmer Keith, Phillip B. Sharpe a Douglas B. Wesson z výrobců střelných zbraní Smith & Wesson a Winchester.
0,38 Speciální: 0,38 Smith & Wesson Special , také běžně známý jako 0,38 S&W Special , 0,38 Special , 0,38 Spl , 0,38 Spc , nebo 9x29mmR je obroučená kazeta se středovým zápalem navržená společností Smith & Wesson. Nejčastěji se používá v revolverech, ačkoli toto kolo používají i některé samonabíjecí pistole a karabiny. 0,38 Special byl standardní servisní kazeta pro drtivou většinu policejních oddělení Spojených států od dvacátých do devadesátých let a byla to také běžná kazeta s pistolí používaná vojenským personálem Spojených států v první světové válce, druhé světové válce, korejské válce a vietnamská válka. V jiných částech světa je znám pod metrickým označením 9 × 29,5 mm R nebo 9,1 × 29 mmR .
Ráže .38: Ráže 0,38 je často používaný název pro ráže střelných zbraní a střelných zbraní.
0,38 Speciální: 0,38 Smith & Wesson Special , také běžně známý jako 0,38 S&W Special , 0,38 Special , 0,38 Spl , 0,38 Spc , nebo 9x29mmR je obroučená kazeta se středovým zápalem navržená společností Smith & Wesson. Nejčastěji se používá v revolverech, ačkoli toto kolo používají i některé samonabíjecí pistole a karabiny. 0,38 Special byl standardní servisní kazeta pro drtivou většinu policejních oddělení Spojených států od dvacátých do devadesátých let a byla to také běžná kazeta s pistolí používaná vojenským personálem Spojených států v první světové válce, druhé světové válce, korejské válce a vietnamská válka. V jiných částech světa je znám pod metrickým označením 9 × 29,5 mm R nebo 9,1 × 29 mmR .
0,4: 0,4 , 0,4 , bod čtyři nebo tečka čtyři mohou odkazovat na: Číslo 0,4 jako zlomkové číslo 0,4 výstřel, basketbalový výstřel hráče Dereka Fishera, který zbývá 0,4 sekundy ve hře 5 semifinále Západní konference NBA 2004 Point4, skladatelský tým z Velké Británie ve složení Pete Day, Phil Dyson, Paul (Bronze) Newton a Daniel Sherman Program Point Four, program technické pomoci pro „rozvojové země", který oznámil prezident Spojených států Harry S. Truman ve svém inauguračním projevu 20. ledna 1949 DOT 4, druh brzdové kapaliny Braillovo písmo, tečky-4, je 6bodová nebo 8bodová braillova buňka se zvednutou horní pravou tečkou
0,45 AKT: 0,45 ACP nebo 0,45 Auto (11,43 × 23 mm) je bezrámová nábojnice s přímými stěnami, navržená Johnem Mosesem Browningem v roce 1904, pro použití v jeho prototypu poloautomatické pistole Colt. Po úspěšných vojenských zkouškách byl přijat jako standardní komora pro Coltovu pistoli M1911. Kolo bylo vyvinuto z důvodu nedostatečné brzdné síly, která se vyskytla v povstání Moro s použitím 0,38 Long Colt. Tato zkušenost a testy Thompson-LaGarde z roku 1904 vedly armádu a kavalérii k rozhodnutí, že u nové zbraně bude vyžadováno minimum kalibru 0,45.
0,4: 0,4 , 0,4 , bod čtyři nebo tečka čtyři mohou odkazovat na: Číslo 0,4 jako zlomkové číslo 0,4 výstřel, basketbalový výstřel hráče Dereka Fishera, který zbývá 0,4 sekundy ve hře 5 semifinále Západní konference NBA 2004 Point4, skladatelský tým z Velké Británie ve složení Pete Day, Phil Dyson, Paul (Bronze) Newton a Daniel Sherman Program Point Four, program technické pomoci pro „rozvojové země", který oznámil prezident Spojených států Harry S. Truman ve svém inauguračním projevu 20. ledna 1949 DOT 4, druh brzdové kapaliny Braillovo písmo, tečky-4, je 6bodová nebo 8bodová braillova buňka se zvednutou horní pravou tečkou
Derek Fisher: Derek Lamar Fisher je americký basketbalový trenér a bývalý hráč, který je hlavním trenérem a generálním manažerem Los Angeles Sparks v Ženské národní basketbalové asociaci (WNBA). Fisher profesionálně hrál v National Basketball Association (NBA) po dobu 18 sezón a většinu své kariéry strávil v Los Angeles Lakers, s nímž vyhrál pět šampionátů NBA. On také hrál za Golden State Warriors, Utah Jazz, Oklahoma City Thunder a Dallas Mavericks. Působil také jako prezident Národní asociace hráčů v basketbalu (NBPA).
Jedna polovina: Jedna polovina je neredukovatelný zlomek vyplývající z dělení jednoho dvěma (2) nebo zlomek vyplývající z dělení libovolného čísla jeho dvojnásobkem. Násobení jednou polovinou je ekvivalentní dělení dvěma nebo „poloviční"; naopak, dělení jednou polovinou se rovná násobení dvěma nebo „zdvojnásobení". Jedna polovina se často objevuje v matematických rovnicích, receptech, měřeních atd. O polovině lze také říci, že je jednou částí něčeho rozděleného na dvě stejné části.
0,50 BMG: Kulomet Browning 0,50 je nábojnice kalibru 0,50 palce (12,7 mm) vyvinutá pro kulomet M2 Browning koncem 10. let 20. století, do oficiální služby je uvedena v roce 1921. Podle STANAG 4383 se jedná o standardní kazetu pro síly NATO jako stejně jako mnoho zemí, které nejsou členy NATO. Samotná kazeta byla vyrobena v mnoha variantách: několik generací pravidelného míče, stopovací, průbojné (AP), zápalné a sabotované náboje podkalibru. Z nábojů určených pro kulomety se pomocí kovových článků vyrábí souvislý pás.
Chlapci protitanková puška: Rifle, Anti-Tank, .55in, Boys , běžně známá jako „Boys Anti-tank Rifle" , byla britská protitanková puška používaná během druhé světové války. Uživatelé jej kvůli své velikosti a velkému otvoru často přezdívali „sloní zbraň".
Euler – Mascheroniho konstanta: Eulerova-Mascheroniho konstanta je matematická konstanta opakující se v analýze a teorii čísel, obvykle označovaná malým řeckým písmenem gama.
Euler – Mascheroniho konstanta: Eulerova-Mascheroniho konstanta je matematická konstanta opakující se v analýze a teorii čísel, obvykle označovaná malým řeckým písmenem gama.
Jedna polovina: Jedna polovina je neredukovatelný zlomek vyplývající z dělení jednoho dvěma (2) nebo zlomek vyplývající z dělení libovolného čísla jeho dvojnásobkem. Násobení jednou polovinou je ekvivalentní dělení dvěma nebo „poloviční"; naopak, dělení jednou polovinou se rovná násobení dvěma nebo „zdvojnásobení". Jedna polovina se často objevuje v matematických rovnicích, receptech, měřeních atd. O polovině lze také říci, že je jednou částí něčeho rozděleného na dvě stejné části.
Kulomet Vickers 0,50: Kulomet Vickers 0,50 , známý také jako „Vickers 0,50", byl podobný kulometu Vickers 0,303 palce (7,70 mm), ale zvětšený, aby používal kulatý 0,5 palcový (12,7 mm) větší kalibr. To vidělo nějaké použití v tancích a jiných bojových vozidlech, ale častěji se používalo jako blízká protiletadlová zbraň na Royal Navy a spojeneckých lodích, obvykle v montáži čtyř zbraní. Vickers vypálil britskou munici 0,50 Vickers (12,7 × 81 mm), ne známější americký 0,50 BMG (12,7 × 99 mm).
0,5 mm: 0,5 mm (0,5 ミ リ) je japonský dramatický film z roku 2014 režírovaný Momoko Ando. To bylo propuštěno v Japonsku 8. listopadu 2014.
0,5 mm: 0,5 mm (0,5 ミ リ) je japonský dramatický film z roku 2014 režírovaný Momoko Ando. To bylo propuštěno v Japonsku 8. listopadu 2014.
Zlatý řez: V matematice jsou dvě veličiny ve zlatém řezu, pokud je jejich poměr stejný jako poměr jejich součtu k větší ze dvou veličin. Obrázek vpravo ilustruje geometrický vztah. Vyjádřeno algebraicky, na množství a a b s a> b> 0,
Kontakt kvantového bodu: Kontakt kvantového bodu ( QPC ) je úzké zúžení mezi dvěma širokými elektricky vodivými oblastmi o šířce srovnatelné s elektronovou vlnovou délkou.
Pravopis kalkulačky: Pravopis kalkulačky je nezamýšlená charakteristika displeje sedmi segmentů, který tradičně používají kalkulačky (O, I, Z, E, H, S, g, L, B, G), ve kterém se při čtení vzhůru nohama číslice podobají písmena latinské abecedy. Každá číslice může být mapována na jedno nebo více písmen, čímž se vytvoří omezená, ale funkční podmnožina abecedy, někdy označovaná jako beghilos .
0,8Syooogeki: 0,8Syooogeki byli dvoučlennou japonskou nezávislou kapelou, která debutovala v roce 2009 singlem „Postman John".
Rychlost filmu: Rychlost filmu je míra citlivosti fotografického filmu na světlo, určená senzitometrií a měřená na různých číselných stupnicích, nejnovější je systém ISO. K popisu vztahu mezi expozicí a světelností výstupního obrazu v digitálních fotoaparátech se používá úzce související systém ISO.
0,8Syooogeki: 0,8Syooogeki byli dvoučlennou japonskou nezávislou kapelou, která debutovala v roce 2009 singlem „Postman John".
0,8Syooogeki: 0,8Syooogeki byli dvoučlennou japonskou nezávislou kapelou, která debutovala v roce 2009 singlem „Postman John".
0,8Syooogeki: 0,8Syooogeki byli dvoučlennou japonskou nezávislou kapelou, která debutovala v roce 2009 singlem „Postman John".
0,8Syooogeki: 0,8Syooogeki byli dvoučlennou japonskou nezávislou kapelou, která debutovala v roce 2009 singlem „Postman John".
0,8Syooogeki: 0,8Syooogeki byli dvoučlennou japonskou nezávislou kapelou, která debutovala v roce 2009 singlem „Postman John".
0,8Syooogeki: 0,8Syooogeki byli dvoučlennou japonskou nezávislou kapelou, která debutovala v roce 2009 singlem „Postman John".
0,9: 0.9 je čtvrté album francouzského rappera Booby a vydáno 24. listopadu 2008 na Tallac Records prostřednictvím hlavní skupiny Barclay Records / Universal Music Group.
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,99: 0,99 může odkazovat se na: 99% (disambiguation) 99p (disambiguation) 99 centů (disambiguation)
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...
0,999 ...: V matematice 0,999 ... označuje opakující se desetinnou čárku skládající se z nekonečně mnoha 9 s za desetinnou čárkou. Toto opakující se desetinné číslo představuje nejmenší číslo, které není menší než každé desetinné číslo v pořadí. Toto číslo se rovná 1. Jinými slovy „0,999 ..." a „1" představují stejné číslo. Existuje mnoho způsobů, jak tuto rovnost ukázat, od intuitivních argumentů až po matematicky důkladné důkazy. Použitá technika závisí na cílovém publiku, předpokladech pozadí, historickém kontextu a preferovaném vývoji reálných čísel, systému, ve kterém je běžně definováno 0,999 ...