Safri Duo, 3.0, 3.0

Safri Duo: Safri Duo je dánské elektronické perkusní duo složené z Uffe Savery a Morten Friis. Zpočátku klasicky orientovaní, později vytvořili skladbu mísící jak kmenový zvuk, tak moderní elektroniku. Vydané v roce 2000 „Played-A-Live" se stalo jednou z nejpopulárnějších písní v Evropě v roce 2001. Z jediného a následného alba Episode II se po celém světě prodalo milion jednotek, čímž se Safri Duo stalo mezinárodně nejúspěšnějším dánským počinem od doby Aqua .
3,0: 3.0 může odkazovat na:
3,0: 3.0 může odkazovat na:
3.0 (profesionální zápas): Ever-Rise , dříve známý jako Team 3.0, je kanadský profesionální wrestlingový značkový tým pocházející z Châteauguay v Quebecu, který se skládá ze Scotta „Jaggeda" Parkera a Shana „Big Magic" Matthewsa. V současné době jsou podepsány s WWE a vystupují na značkách NXT a 205 Live pod jmény ringu Chase Parker a Matt Martel .
3.0 (profesionální zápas): Ever-Rise , dříve známý jako Team 3.0, je kanadský profesionální wrestlingový značkový tým pocházející z Châteauguay v Quebecu, který se skládá ze Scotta „Jaggeda" Parkera a Shana „Big Magic" Matthewsa. V současné době jsou podepsány s WWE a vystupují na značkách NXT a 205 Live pod jmény ringu Chase Parker a Matt Martel .
3bodový hráč: Tříbodový hráč je sportovní klasifikace postižení pro basketbal na vozíku. Lidé v této třídě mají dobrý pohyb kmene dopředu a dozadu, ale špatný až žádný pohyb kmene do strany. Třída zahrnuje lidi s paraplegií a amputacemi L2-L4. Po amputaci jsou do této třídy zařazováni obecně, pokud mají disartikulace kyčle nebo únosy kyčle. Hráči v této třídě mohou obecně odskakovat míčky, které jsou nad jejich hlavami, ale při bočních doskokech mohou mít problémy s rovnováhou.
3.1: 3.1 může odkazovat na: Aproximace matematické konstanty π Zkrácený odkaz na vydání 3.1 nějakého softwaru, jako je Windows 3.1x
3:10 do Yumy: 3:10 pro Yumu může odkazovat na: "Tři-deset k Yumě", 1953 západní povídky Elmora Leonarda 3:10 pro Yumu , režie Delmer Daves a v hlavní roli Glenn Ford a Van Heflin 3:10 pro Yumu , remake filmu z roku 1957 v režii Jamese Mangolda v hlavní roli s Russellem Crowem a Christianem Baleem „The 3:10 to Yuma" (píseň), píseň od George Duninga a Neda Washingtona, kterou nahrál Frankie Laine
Zemětřesení a tsunami v tohoku v roce 2011: Zemětřesení v roce 2011 u tichomořského pobřeží Tōhoku bylo podmořské zemětřesení o velikosti 9,0–9,1 (M w ) u japonského pobřeží, ke kterému došlo v pátek 11. března 2011 v 14:46 JST, s epicentrem přibližně 70 kilometrů východně od poloostrova Oshika v Tōhoku a hypocentrum v podvodní hloubce přibližně 29 km (18 mi).
3.11: Přežít Japonsko: 3.11: Přežít Japonsko je dokumentární film o zemětřesení a tsunami v Tóhoku v roce 2011 a jaderné katastrofě Fukušima Daiiči v Japonsku, jehož autorem a režisérem je dobrovolník a obyvatel Christopher Noland.
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
3. 1415 (album): 3.1415 je debutové studiové album tchajwanské umělkyně Mandopop Seliny Jen z dívčí skupiny SHE. Vydalo ji 9. ledna 2015 společnost HIM International Music.
3. 1415 (album): 3.1415 je debutové studiové album tchajwanské umělkyně Mandopop Seliny Jen z dívčí skupiny SHE. Vydalo ji 9. ledna 2015 společnost HIM International Music.
3. 1415 (album): 3.1415 je debutové studiové album tchajwanské umělkyně Mandopop Seliny Jen z dívčí skupiny SHE. Vydalo ji 9. ledna 2015 společnost HIM International Music.
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
Důkaz, že 22/7 překračuje π: Důkazy matematického takže racionální číslo 22/7 je větší než n (pi) sahají až do starověku. Jeden z těchto důkazů, který byl nedávno vyvinut, ale vyžaduje pouze základní techniky z počtu, přitahoval pozornost v moderní matematice díky své matematické eleganci a svým souvislostem s teorií diofantických aproximací. Stephen Lucas nazývá tento důkaz „jedním z nejkrásnějších výsledků souvisejících s aproximací π ". Julian Havil končí diskusi o pokračujících zlomkových aproximacích π s výsledkem, který jej v tomto kontextu popisuje jako „nemožné odolat zmínce".
3.14 (EP): 3.14 je debutové EP kanadského rappera Pvrxe. To bylo propuštěno 26. července 2019, Def Jam Recordings.
3.14 (EP): 3.14 je debutové EP kanadského rappera Pvrxe. To bylo propuštěno 26. července 2019, Def Jam Recordings.
Pi: Číslo π je matematická konstanta. Je definován jako poměr obvodu kruhu k jeho průměru a má také různé ekvivalentní definice. Objevuje se v mnoha vzorcích ve všech oblastech matematiky a fyziky a nejstarší známé použití řeckého písmene π k vyjádření poměru obvodu kruhu k jeho průměru bylo podle velšského matematika Williama Jonese v roce 1706. To je přibližně 3,14159. Od poloviny 18. století je reprezentován řeckým písmenem „ π " a je koncipován jako „ pi ". To je také označováno jako Archimedova konstanta .
3.15.20: 3.15.20 je čtvrté studiové album amerického rappera Donalda Glovera pod uměleckým jménem Childish Gambino. Původně byl nahrán na web donaldgloverpresents.com 15. března 2020, poté byl odstraněn o 12 hodin později; bylo proto označováno jako Donald Glover Presents . Po odpočítávání bylo 22. března vydáno ke streamovacím a stahovacím službám pod názvem 3.15.20 . Album obsahuje hostující vystoupení od Ariany Grande, Kadhja Boneta, 21 Savage a Ink. Glover produkoval album s řadou spolupracovníků, včetně DJ Dahi, dlouholetý producent Ludwig Göransson, Chukwudi Hodge, Kurtis McKenzie a James Francies, Jr.
3.15.20: 3.15.20 je čtvrté studiové album amerického rappera Donalda Glovera pod uměleckým jménem Childish Gambino. Původně byl nahrán na web donaldgloverpresents.com 15. března 2020, poté byl odstraněn o 12 hodin později; bylo proto označováno jako Donald Glover Presents . Po odpočítávání bylo 22. března vydáno ke streamovacím a stahovacím službám pod názvem 3.15.20 . Album obsahuje hostující vystoupení od Ariany Grande, Kadhja Boneta, 21 Savage a Ink. Glover produkoval album s řadou spolupracovníků, včetně DJ Dahi, dlouholetý producent Ludwig Göransson, Chukwudi Hodge, Kurtis McKenzie a James Francies, Jr.
3.1: 3.1 může odkazovat na: Aproximace matematické konstanty π Zkrácený odkaz na vydání 3.1 nějakého softwaru, jako je Windows 3.1x
USB 3.0: USB 3.0 je třetí hlavní verze standardu USB (Universal Serial Bus) pro propojení počítačů a elektronických zařízení. Mezi další vylepšení přidává USB 3.0 novou přenosovou rychlost označovanou jako SuperSpeed ​​USB (SS), která dokáže přenášet data rychlostí až 5 Gbit / s (625 MB / s), což je přibližně 10krát rychlejší než standard USB 2.0. Doporučuje se, aby výrobci odlišili konektory USB 3.0 od svých protějšků USB 2.0 pomocí modré barvy pro zásuvky a zástrčky Standard-A a iniciál SS .
Phillip Lim: Phillip Lim je americký módní návrhář čínského původu, jehož rodiče se během kambodžské genocidy přistěhovali do Ameriky z Thajska. Lim spoluzaložil a pracoval v losangeleské módní značce Development od roku 2000 do roku 2004. Na podzim roku 2005 spolu s přítelem a obchodním partnerem Wen Zhouem založil společnost 3.1 Phillip Lim a stal se kreativním zástupcem společnosti.
Phillip Lim: Phillip Lim je americký módní návrhář čínského původu, jehož rodiče se během kambodžské genocidy přistěhovali do Ameriky z Thajska. Lim spoluzaložil a pracoval v losangeleské módní značce Development od roku 2000 do roku 2004. Na podzim roku 2005 spolu s přítelem a obchodním partnerem Wen Zhouem založil společnost 3.1 Phillip Lim a stal se kreativním zástupcem společnosti.
Nízkoalkoholické pivo: Pivo s nízkým obsahem alkoholu je pivo s malým nebo žádným obsahem alkoholu a jeho cílem je reprodukovat chuť piva a současně eliminovat opojné účinky standardních alkoholických nápojů. Většina piv s nízkým obsahem alkoholu jsou ležáky, ale existují i ​​některá piva s nízkým obsahem alkoholu. Nízkoalkoholické pivo je také známé jako světlé pivo , nealkoholické pivo , malé pivo , malé pivo nebo téměř pivo .
3,2palcová zbraň M1897: 3,2palcové dělo M1897 (81 mm), se svými předchůdci M1885 a M1890 , bylo první americkou armádou jako první ocelová, loupená, závěrová polní zbraň. Jednalo se o primární polní dělostřelectvo armády ve španělsko-americké válce, filipínsko-americké válce a boxerském povstání od roku 1898 do roku 1902.
3,2palcová zbraň M1897: 3,2palcové dělo M1897 (81 mm), se svými předchůdci M1885 a M1890 , bylo první americkou armádou jako první ocelová, loupená, závěrová polní zbraň. Jednalo se o primární polní dělostřelectvo armády ve španělsko-americké válce, filipínsko-americké válce a boxerském povstání od roku 1898 do roku 1902.
3,2palcová zbraň M1897: 3,2palcové dělo M1897 (81 mm), se svými předchůdci M1885 a M1890 , bylo první americkou armádou jako první ocelová, loupená, závěrová polní zbraň. Jednalo se o primární polní dělostřelectvo armády ve španělsko-americké válce, filipínsko-americké válce a boxerském povstání od roku 1898 do roku 1902.
3.2.1 .: 3.2.1. je debutové album rockové kapely Zilch, vydané 23. července 1998. Je to jejich jediné dílo s původní frontmanskou kůží, kvůli jeho smrti dva měsíce před vydáním. Album dosáhlo čísla 2 na žebříčku Oricon, bylo 54 nejprodávanějším albem roku a RIAJ získalo certifikaci Double Platinum za prodej přes 800 000.
3.2.1 .: 3.2.1. je debutové album rockové kapely Zilch, vydané 23. července 1998. Je to jejich jediné dílo s původní frontmanskou kůží, kvůli jeho smrti dva měsíce před vydáním. Album dosáhlo čísla 2 na žebříčku Oricon, bylo 54 nejprodávanějším albem roku a RIAJ získalo certifikaci Double Platinum za prodej přes 800 000.
3.2.1 .: 3.2.1. je debutové album rockové kapely Zilch, vydané 23. července 1998. Je to jejich jediné dílo s původní frontmanskou kůží, kvůli jeho smrti dva měsíce před vydáním. Album dosáhlo čísla 2 na žebříčku Oricon, bylo 54 nejprodávanějším albem roku a RIAJ získalo certifikaci Double Platinum za prodej přes 800 000.
Protiletadlová cílová raketa M2: Anti-Aircraft Target Rocket M2 byla 3,25 palce (83 mm) raketa vyvinutá a používaná armádou Spojených států během druhé světové války. Byl navržen tak, aby sloužil jako cvičný cíl pro protiletadlová děla, schopný simulovat útoky nízko letících letadel. Přední část rakety byla ogivální a byla opatřena nadrozměrnými ploutvemi, které pomáhaly při sledování rakety účastníky.
Protiletadlová cílová raketa M2: Anti-Aircraft Target Rocket M2 byla 3,25 palce (83 mm) raketa vyvinutá a používaná armádou Spojených států během druhé světové války. Byl navržen tak, aby sloužil jako cvičný cíl pro protiletadlová děla, schopný simulovat útoky nízko letících letadel. Přední část rakety byla ogivální a byla opatřena nadrozměrnými ploutvemi, které pomáhaly při sledování rakety účastníky.
Nízkoalkoholické pivo: Pivo s nízkým obsahem alkoholu je pivo s malým nebo žádným obsahem alkoholu a jeho cílem je reprodukovat chuť piva a současně eliminovat opojné účinky standardních alkoholických nápojů. Většina piv s nízkým obsahem alkoholu jsou ležáky, ale existují i ​​některá piva s nízkým obsahem alkoholu. Nízkoalkoholické pivo je také známé jako světlé pivo , nealkoholické pivo , malé pivo , malé pivo nebo téměř pivo .
3,2palcová zbraň M1897: 3,2palcové dělo M1897 (81 mm), se svými předchůdci M1885 a M1890 , bylo první americkou armádou jako první ocelová, loupená, závěrová polní zbraň. Jednalo se o primární polní dělostřelectvo armády ve španělsko-americké válce, filipínsko-americké válce a boxerském povstání od roku 1898 do roku 1902.
Nízkoalkoholické pivo: Pivo s nízkým obsahem alkoholu je pivo s malým nebo žádným obsahem alkoholu a jeho cílem je reprodukovat chuť piva a současně eliminovat opojné účinky standardních alkoholických nápojů. Většina piv s nízkým obsahem alkoholu jsou ležáky, ale existují i ​​některá piva s nízkým obsahem alkoholu. Nízkoalkoholické pivo je také známé jako světlé pivo , nealkoholické pivo , malé pivo , malé pivo nebo téměř pivo .
3.3: 3.3 může odkazovat na: Motor Chrysler 3.3, první vlastní domácí pohon 60 kol V6 s pohonem předních kol Chrysler K Desktop Environment 3.3, čtvrté vydání ve třetí sérii vydání K Desktop Environment
Neohexen: Neohexene je organická sloučenina obecného vzorce (CH 3) 3 CCH = CH 2. Je to bezbarvá kapalina, která má podobné vlastnosti jako jiné hexeny. Je předchůdcem komerčních syntetických pižmových parfémů.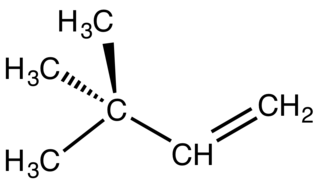
Pravidelný dvacetistěn: V geometrii je pravidelný dvacetistěn konvexní mnohostěn s 20 plochami, 30 hranami a 12 vrcholy. Je to jeden z pěti platonických těles a ten, který má nejvíce tváří.
3.3: 3.3 může odkazovat na: Motor Chrysler 3.3, první vlastní domácí pohon 60 kol V6 s pohonem předních kol Chrysler K Desktop Environment 3.3, čtvrté vydání ve třetí sérii vydání K Desktop Environment
Volt: Volt je odvozená jednotka elektrického potenciálu, rozdílu elektrického potenciálu (napětí) a elektromotorické síly. Je pojmenována po italském fyzikovi Alessandrovi Voltovi (1745–1827).
Disketa: Disketa nebo disketa je typ diskového úložiště složeného z tenkého a pružného disku magnetického paměťového média ve čtvercovém nebo téměř čtvercovém plastovém krytu vyloženém látkou, která odstraňuje prachové částice z rotujícího disku. Diskety jsou čteny a zapisovány na disketovou jednotku ( FDD ).
3,5palcová dopředu střílející raketa letadla: 3,5palcová dopředu střílející letecká raketa nebo 3,5palcová FFAR byla americká raketa vyvinutá během druhé světové války, aby umožnila letadlům útočit na nepřátelské ponorky na dostřel. Raketa prokázala provozní úspěch a vytvořila několik vylepšených verzí pro použití proti pozemním a pozemním cílům.
Disketa: Disketa nebo disketa je typ diskového úložiště složeného z tenkého a pružného disku magnetického paměťového média ve čtvercovém nebo téměř čtvercovém plastovém krytu vyloženém látkou, která odstraňuje prachové částice z rotujícího disku. Diskety jsou čteny a zapisovány na disketovou jednotku ( FDD ).
Disketa: Disketa nebo disketa je typ diskového úložiště složeného z tenkého a pružného disku magnetického paměťového média ve čtvercovém nebo téměř čtvercovém plastovém krytu vyloženém látkou, která odstraňuje prachové částice z rotujícího disku. Diskety jsou čteny a zapisovány na disketovou jednotku ( FDD ).
Pozice disku: Pozice jednotky je oblast standardní velikosti pro přidání hardwaru k počítači. Většina pozic pro disky je připevněna k vnitřku pouzdra, ale některé lze vyjmout.
Disketa: Disketa nebo disketa je typ diskového úložiště složeného z tenkého a pružného disku magnetického paměťového média ve čtvercovém nebo téměř čtvercovém plastovém krytu vyloženém látkou, která odstraňuje prachové částice z rotujícího disku. Diskety jsou čteny a zapisovány na disketovou jednotku ( FDD ).
Disketa: Disketa nebo disketa je typ diskového úložiště složeného z tenkého a pružného disku magnetického paměťového média ve čtvercovém nebo téměř čtvercovém plastovém krytu vyloženém látkou, která odstraňuje prachové částice z rotujícího disku. Diskety jsou čteny a zapisovány na disketovou jednotku ( FDD ).
Disketa: Disketa nebo disketa je typ diskového úložiště složeného z tenkého a pružného disku magnetického paměťového média ve čtvercovém nebo téměř čtvercovém plastovém krytu vyloženém látkou, která odstraňuje prachové částice z rotujícího disku. Diskety jsou čteny a zapisovány na disketovou jednotku ( FDD ).
Disketa: Disketa nebo disketa je typ diskového úložiště složeného z tenkého a pružného disku magnetického paměťového média ve čtvercovém nebo téměř čtvercovém plastovém krytu vyloženém látkou, která odstraňuje prachové částice z rotujícího disku. Diskety jsou čteny a zapisovány na disketovou jednotku ( FDD ).
Disketa: Disketa nebo disketa je typ diskového úložiště složeného z tenkého a pružného disku magnetického paměťového média ve čtvercovém nebo téměř čtvercovém plastovém krytu vyloženém látkou, která odstraňuje prachové částice z rotujícího disku. Diskety jsou čteny a zapisovány na disketovou jednotku ( FDD ).
Nikon AF-S DX Zoom-Nikkor 18-300 mm f / 3,5-6,3G ED VR: Objektiv 18–300 mm f / 3,5–6,3 G je teleobjektiv se superzoomem vyráběný společností Nikon pro řadu fotoaparátů DX DSLR.
3,5palcová dopředu střílející raketa letadla: 3,5palcová dopředu střílející letecká raketa nebo 3,5palcová FFAR byla americká raketa vyvinutá během druhé světové války, aby umožnila letadlům útočit na nepřátelské ponorky na dostřel. Raketa prokázala provozní úspěch a vytvořila několik vylepšených verzí pro použití proti pozemním a pozemním cílům.
3,5palcová dopředu střílející raketa letadla: 3,5palcová dopředu střílející letecká raketa nebo 3,5palcová FFAR byla americká raketa vyvinutá během druhé světové války, aby umožnila letadlům útočit na nepřátelské ponorky na dostřel. Raketa prokázala provozní úspěch a vytvořila několik vylepšených verzí pro použití proti pozemním a pozemním cílům.
Serial ATA: Serial ATA je rozhraní počítačové sběrnice, které připojuje adaptéry hostitelské sběrnice k velkokapacitním paměťovým zařízením, jako jsou jednotky pevných disků, optické jednotky a jednotky SSD. Serial ATA následoval dřívější standard Parallel ATA (PATA), aby se stal převládajícím rozhraním pro úložná zařízení.
Disketa: Disketa nebo disketa je typ diskového úložiště složeného z tenkého a pružného disku magnetického paměťového média ve čtvercovém nebo téměř čtvercovém plastovém krytu vyloženém látkou, která odstraňuje prachové částice z rotujícího disku. Diskety jsou čteny a zapisovány na disketovou jednotku ( FDD ).
Disketa: Disketa nebo disketa je typ diskového úložiště složeného z tenkého a pružného disku magnetického paměťového média ve čtvercovém nebo téměř čtvercovém plastovém krytu vyloženém látkou, která odstraňuje prachové částice z rotujícího disku. Diskety jsou čteny a zapisovány na disketovou jednotku ( FDD ).
Pancéřová pěst: Bazooka (/ bəˈzu ː k) /) je běžný název pro přenosnou bezzákluzovou protitankovou raketometovou zbraň, široce nasazenou armádou Spojených států, zejména během druhé světové války. Inovativní bazuka, označovaná také jako „Stovepipe", patřila k první generaci protitankových zbraní s raketovým pohonem používaných v pěchotním boji. Díky raketě na tuhý pohon umožňovala dodávat vysoce výbušné protitankové hlavice (HEAT) proti obrněným vozidlům, kulometným hnízdům a opevněným bunkrům v dosahu přesahujícím standardní vrhaný granát nebo důl. Všeobecně používaná přezdívka vznikla z neurčité podoby varianty M1 s hudebním nástrojem zvaným „bazuka", který vynalezl a popularizoval americký komik Bob Burns z 30. let.
Vysokorychlostní paketový přístup: High Speed ​​Packet Access ( HSPA ) je sloučením dvou mobilních protokolů, High Speed ​​Downlink Packet Access (HSDPA) a High Speed ​​Uplink Packet Access (HSUPA), které rozšiřují a zlepšují výkon stávajících mobilních telekomunikačních sítí 3G pomocí protokolů WCDMA. Další vylepšený standard 3GPP, Evolve High Speed ​​Packet Access, byl vydán koncem roku 2008 s následným celosvětovým přijetím počínaje rokem 2010. Novější standard umožňuje, aby bitové rychlosti dosáhly až 337 Mbit / s při downlinku a 34 Mbit / s v uplink. Těchto rychlostí se však v praxi dosahuje jen zřídka.
Vysokorychlostní paketový přístup: High Speed ​​Packet Access ( HSPA ) je sloučením dvou mobilních protokolů, High Speed ​​Downlink Packet Access (HSDPA) a High Speed ​​Uplink Packet Access (HSUPA), které rozšiřují a zlepšují výkon stávajících mobilních telekomunikačních sítí 3G pomocí protokolů WCDMA. Další vylepšený standard 3GPP, Evolve High Speed ​​Packet Access, byl vydán koncem roku 2008 s následným celosvětovým přijetím počínaje rokem 2010. Novější standard umožňuje, aby bitové rychlosti dosáhly až 337 Mbit / s při downlinku a 34 Mbit / s v uplink. Těchto rychlostí se však v praxi dosahuje jen zřídka.
Boyce – Codd normální forma: Normální forma Boyce – Codd je normální forma používaná při normalizaci databáze. Jedná se o mírně silnější verzi třetí normální formy (3NF). BCNF byl vyvinut v roce 1974 Raymondem F. Boycem a Edgarem F. Coddem k řešení určitých typů anomálií, kterými se 3NF nezabývá, jak bylo původně definováno.
Disketa: Disketa nebo disketa je typ diskového úložiště složeného z tenkého a pružného disku magnetického paměťového média ve čtvercovém nebo téměř čtvercovém plastovém krytu vyloženém látkou, která odstraňuje prachové částice z rotujícího disku. Diskety jsou čteny a zapisovány na disketovou jednotku ( FDD ).
Modelové váhy pro železniční dopravu: Modelování železniční dopravy používá různé stupnice, aby zajistilo, že zmenšené modely vypadají správně, pokud jsou umístěny vedle sebe. Váhy modelových železnic jsou celosvětově standardizovány mnoha organizacemi a fandy. Některé stupnice jsou uznávány globálně, zatímco jiné jsou méně rozšířené a v mnoha případech mimo kruh jejich původu téměř neznámé. Váhy mohou být vyjádřeny jako číselný poměr nebo jako písmena definovaná ve standardech modelování železniční dopravy Většina výrobců komerčních modelů železničních zařízení vychází při své nabídce ze standardů Normen Europäischer Modellbahnen (NEM) nebo National Model Railroad Association (NMRA) v nejpopulárnějších měřítcích.
Disketa: Disketa nebo disketa je typ diskového úložiště složeného z tenkého a pružného disku magnetického paměťového média ve čtvercovém nebo téměř čtvercovém plastovém krytu vyloženém látkou, která odstraňuje prachové částice z rotujícího disku. Diskety jsou čteny a zapisovány na disketovou jednotku ( FDD ).
Disketa: Disketa nebo disketa je typ diskového úložiště složeného z tenkého a pružného disku magnetického paměťového média ve čtvercovém nebo téměř čtvercovém plastovém krytu vyloženém látkou, která odstraňuje prachové částice z rotujícího disku. Diskety jsou čteny a zapisovány na disketovou jednotku ( FDD ).
3,5 mm: Rozměr 3,5 mm nebo 3,5 mm může odkazovat na: Měřítko HO, v modelování železniční dopravy, měřítko 1:87, s kolejnicemi 16,5 mm od sebe, představující standardní rozchod 3,5 mm jack, používaný na audio a mobilních telefonních zařízeních
Telefonní konektor (audio): Telefonní konektor , známý také jako telefonní konektor , zvukový konektor , konektor pro sluchátka nebo konektor , je skupina elektrických konektorů, které se obvykle používají pro analogové zvukové signály. Standardem je, že zástrčka se připojí ke konektoru.
Telefonní konektor (audio): Telefonní konektor , známý také jako telefonní konektor , zvukový konektor , konektor pro sluchátka nebo konektor , je skupina elektrických konektorů, které se obvykle používají pro analogové zvukové signály. Standardem je, že zástrčka se připojí ke konektoru.
3,5 mm: Rozměr 3,5 mm nebo 3,5 mm může odkazovat na: Měřítko HO, v modelování železniční dopravy, měřítko 1:87, s kolejnicemi 16,5 mm od sebe, představující standardní rozchod 3,5 mm jack, používaný na audio a mobilních telefonních zařízeních
3,5 mm: Rozměr 3,5 mm nebo 3,5 mm může odkazovat na: Měřítko HO, v modelování železniční dopravy, měřítko 1:87, s kolejnicemi 16,5 mm od sebe, představující standardní rozchod 3,5 mm jack, používaný na audio a mobilních telefonních zařízeních
Telefonní konektor (audio): Telefonní konektor , známý také jako telefonní konektor , zvukový konektor , konektor pro sluchátka nebo konektor , je skupina elektrických konektorů, které se obvykle používají pro analogové zvukové signály. Standardem je, že zástrčka se připojí ke konektoru.
Telefonní konektor (audio): Telefonní konektor , známý také jako telefonní konektor , zvukový konektor , konektor pro sluchátka nebo konektor , je skupina elektrických konektorů, které se obvykle používají pro analogové zvukové signály. Standardem je, že zástrčka se připojí ke konektoru.
3.6.3: 3.6.3 je páté živé album francouzské new wave kapely Indochine. To bylo propuštěno v roce 2003.
XOXO (album): XOXO je debutové studiové album jihokorejsko-čínské chlapecké skupiny Exo, vydané 3. června 2013 společností SM Entertainment a distribuované společností KT Music. Album navazuje na debutové EP skupiny Mama (2012). Album vyšlo ve dvou verzích - korejské vydání „Kiss" a čínské vydání „Hug".
3,67 m dalekohled s pokročilým elektrooptickým systémem: 3,67 m pokročilý elektrooptický systémový dalekohled je dalekohled ministerstva obrany na observatoři Haleakala. Dalekohled je součástí komplexu Maui Space Surveillance Complex (MSSC), který je zase součástí optického a superpočítacího místa Air Force Maui (AMOS).
3,67 m dalekohled s pokročilým elektrooptickým systémem: 3,67 m pokročilý elektrooptický systémový dalekohled je dalekohled ministerstva obrany na observatoři Haleakala. Dalekohled je součástí komplexu Maui Space Surveillance Complex (MSSC), který je zase součástí optického a superpočítacího místa Air Force Maui (AMOS).
Optický dalekohled Devasthal 3,6 m: Optický dalekohled Devasthal 3,6 m je dalekohled Ritchey – Chrétien s čistou aperturou, který postavil Aryabhatta Research Institute of Observational Sciences (ARIES) a je umístěn v lokalitě Devasthal Observatory poblíž Nainitalu v Uttarakhandu v Indii. ARIES provozuje další 1,3m dalekohled na stejném místě. Dalekohled aktivovali na dálku 31. března 2016 indický předseda vlády Narendra Modi a belgický předseda vlády Charles Michel z Bruselu. Optika dalekohledu byla postavena ve spolupráci s belgickou firmou Advanced Mechanical and Optical System (AMOS).
Optický dalekohled Devasthal 3,6 m: Optický dalekohled Devasthal 3,6 m je dalekohled Ritchey – Chrétien s čistou aperturou, který postavil Aryabhatta Research Institute of Observational Sciences (ARIES) a je umístěn v lokalitě Devasthal Observatory poblíž Nainitalu v Uttarakhandu v Indii. ARIES provozuje další 1,3m dalekohled na stejném místě. Dalekohled aktivovali na dálku 31. března 2016 indický předseda vlády Narendra Modi a belgický předseda vlády Charles Michel z Bruselu. Optika dalekohledu byla postavena ve spolupráci s belgickou firmou Advanced Mechanical and Optical System (AMOS).
Horská houfnice QF 3,7 palce: Ordnance, QF 3,7-palcová houfnice je horská zbraň, kterou používají britské armády a armády Commonwealthu v první a druhé světové válce a mezi válkami.
Horská houfnice QF 3,7 palce: Ordnance, QF 3,7-palcová houfnice je horská zbraň, kterou používají britské armády a armády Commonwealthu v první a druhé světové válce a mezi válkami.